Utilizing a bi-kinematic hardening material model in paper modeling is crucial to accurately predict the paper's behavior under various mechanical loadings. This approach integrates both isotropic and kinematic hardening, hence offering a detailed insight into the evolution of the material's yield surface during the deformation process. This model combines two distinct hardening mechanisms: isotropic hardening and kinematic hardening, to provide a more comprehensive description of a material’s behavior under cyclic loading conditions (Figure). In the context of this model:
Isotropic Hardening: This aspect considers the uniform expansion of the yield surface in the stress space. Essentially, it portrays how a material hardens uniformly when exposed to plastic deformation, leading to an increase in yield stress.
Kinematic Hardening: This aspect focuses on the translation of the yield surface in the stress space, depicting the alignment of the material's internal structure as it undergoes deformation. It helps in describing phenomena such as the Bauschinger effect, where a material exhibits different yield stresses under reversed loading due to the translation of the yield surface.

This type of material model was successfully applied in this paper to determine the mechanical behaviours of paper pulp under different forces and deformations. Paper pulp, which primarily comprises of cellulose fibers, is a complex material whose characteristics are markedly non-linear, anisotropic, and viscoelastic. At the macroscopic scale, the paper pulp is considered as a continuum, where the focus is primarily on its bulk properties. The modeling here takes into account the overall response of the paper pulp to external forces, including its elastic, plastic, and viscous behaviours. Using bi-kinematic hardening material model, it is possible to model and anticipate how the pulp material will behave during mechanical loads, taking into consideration factors like density, fibre orientation, and moisture content, which significantly affect the pulp's mechanical characteristics.
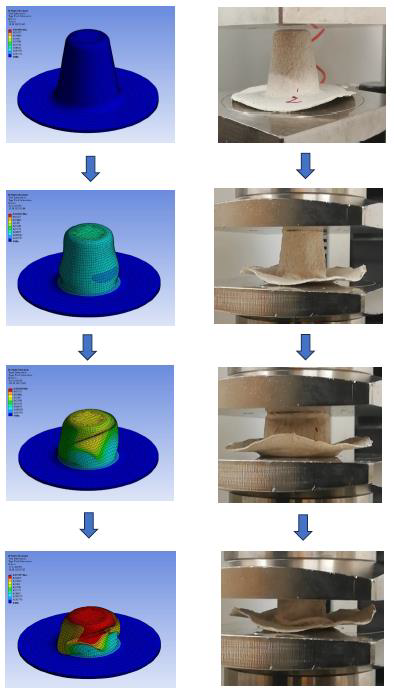
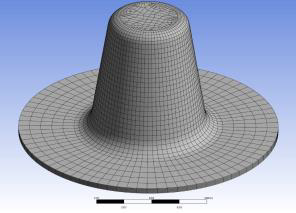
The development of numerical model began with the CAD model of analysed pots. The CAD model of the pot is presented in the left figure and the corresponding FEM model is presented in the right figure. The elements used in numerical simulation were shell elements in order to improve the computational efficiency and convergence of numerical model.

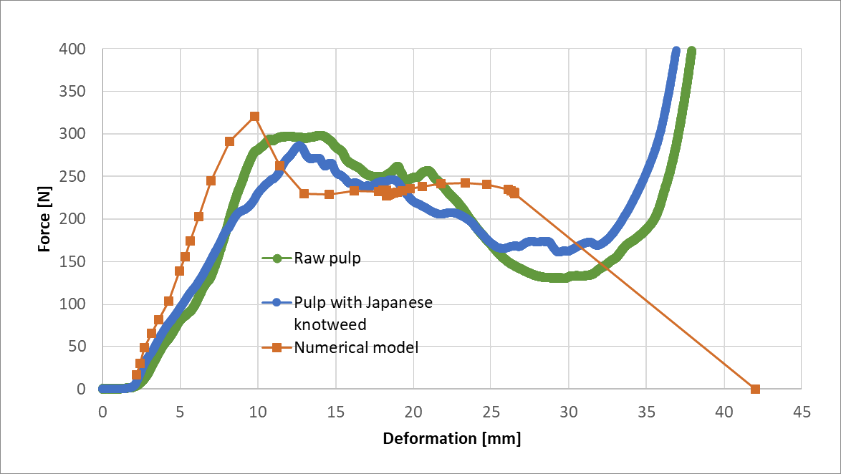
The material properties of pulp were determined by updating the numerical model with real-time data obtained from actual pulp force-deformation measurement. This iterative process, which integrates experimental data into the computational framework, allows for a more precise and reliable prediction of the pulp's performance in various applications. Based on this optimization process finally the material parameters of pulp material were deduced as indicated in the table.
| Parameter | Value | Unit |
|---|---|---|
| density | 650,1 | MPa |
| Young modulus | 50,5 | MPa |
| Poisson ratio | 0,01 | |
| resistance to compression | 1,72*107 | Pa |
| Shear modulus | 2,5*107 | Pa |
| Yield strength | 0,075 | MPa |
| Tangent modulus | 100 | MPa |
The correlation between the deformation data from the numerical model and the results obtained from experimental observations at various load stages are presented in the left figure below. By adopting the identified material parameters defined in the above table a high degree of correlation between the simulated and experimentally obtained behaviour can be observed. In addition, the numerically predicted and experimentally obtained deformation-force curve are presented in the right figure below.